НовостиNews
-
ПоискSearch
-
ТекстыTexts
-
ФотоPhotos
-
КартыMaps
-
СнаряжениеEquipment
-
LTLT
Setup for measuring surface areas (for heat exchangers and aerogel sample) and volumes. The cell with measured sample is connected to a pressure gauge, piston for changing/measuring volume and port for pumping the system and filling it with dry nitrogen (we use nitrogen evaporating from a dewar). The cell can be dipped in liquid nitrogen. Two cells have been made, with inner sizes 12x12x76 mm and 2x20x60 mm.
Part list:
General idea of the measurement is following: the cell with the sample is filled with dry nitrogen. Amount of gas can be calculated if temperature, pressure and volume is known. Then the cell is cooled down to 77K, and pressure change is recorded. Pressure changes because of two effects: cooling of gas in the cold volume and gas adsorption. The first effect can be calculated from known volumes, temperatures and pressures, the second one is proportional to the surface area to be measured.
Volume of the cell ("cold volume") should be reduced as much as possible. For measuring area of the order of 1m$^2$ it's good to have cold volume less then 1 ml.
Hot volume of the system should be chosen according with the measured area. If the volume is too large then pressure change is small, if it is too small then almost all gas will be adsorbed. In both cases it will be hard to do the measurement. Reasonable value for the hot volume is about 1 ml per 1m^2 of measured area. It can be adjusted using the piston.
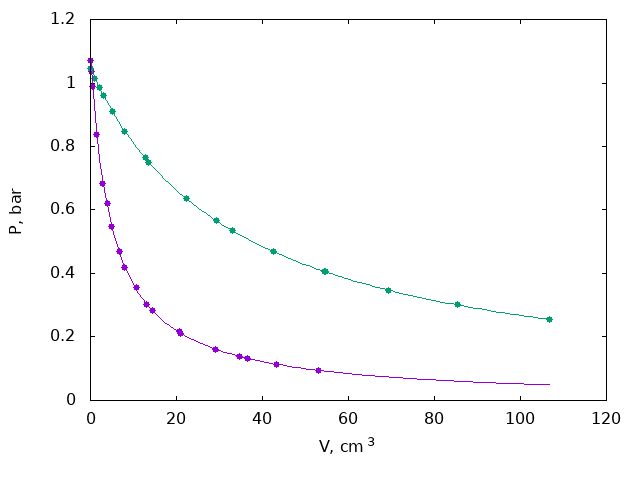
Both volumes are measured by moving the piston and recording pressure as a function of volume and fitting it with the function $P = A/(V+V_0) + P_0$ with 3 parameters ($A$, $P_0$, $V_0$). Here $V_0$ is the volume to be measured, $P_0$ is zero of the pressure gauge, this parameter can be fixed if it is known.
Cooling of the cell in liquid nitrogen takes about 5 ... 30 minutes depending on the sample (for nuclear stage blocks in 12x12x76 cell it was long). Warming can be done quite fast with a heat gun. Final thermalization to room temperature can be done with a fan. One should wait long enough until pressure reach the equilibrium. (TODO: Should we install PT1000 thermometer on the cell?). In this method it is possible to measure two points in the cycle: start with some pressure, cool down, remove/add some gas, wait until equilibrium is reached, warm up, measure new pressure.
There are a few ways how measurements can be done. One option (constant volume measurement) is described above. Another is constant-pressure measurement: start with large enough volume, after cooling move the piston to keep original pressure. This method can eliminate some pressure-dependent effects such as volume changing due to material elasticity, gas adsorption in hot parts of the system etc ("acrylic tube problem"). It is also possible to move the piston after cooling and record pressure as a function of the piston position, measuring many points n a single cooling cycle. In any case one should calculate amount of adsorbed gas as a function of pressure. This is an "adsorption isotherm" which is described by BET model.
It is convenient to collect data as a table with following columns:
Then amount of adsorbed gas can be calculated as $$ n_{ads} = \left( \frac{P_h (V_t+X_h k)}{T_h} - \frac{P_c (V_t-V_h)}{T_c} - \frac{P_c (V_h+X_c k)}{T_h} \right)\ \frac{1}{R} $$ Where $T_h$ and $T_c$ are room temperature and temperature of liquid nitrogen, $k$ is conversion coefficient between piston position and volume (cross-section of the tube). Conversion coefficient for $PV$: 1 Pa m$^3$ = 0.1 bar ml
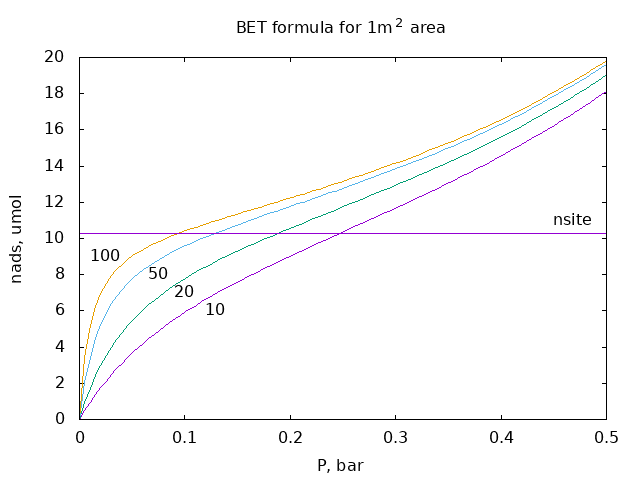
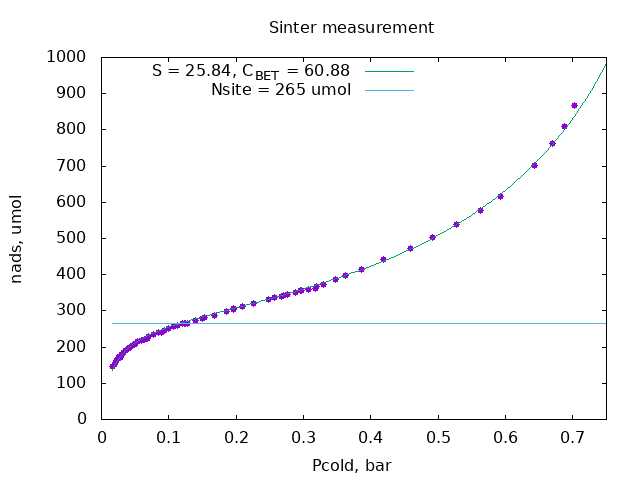
In the BET model amount of adsorbed gas iы given by the formula: $$ n_{ads}(P) = n_{site} \frac{C\,P}{P_0 -P}\ \frac{1}{1+(C-1)\,P/P_0} $$ where $n_{site}$ is amount of adsorption sites, each corresponds to $0.162\cdot10^{-18}$ m$^2$ area, $P_0$ is condensation pressure of the gas, 1 bar in our case, and $C$ is the model parameter, slope at $P=0$.
