НовостиNews
-
ПоискSearch
-
ТекстыTexts
-
ФотоPhotos
-
КартыMaps
-
СнаряжениеEquipment
-
LTLT
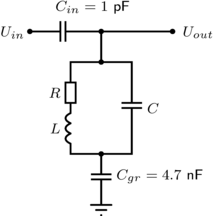
For the circuit on the figure we have three equations:
1. Voltage across the LC-circuit, same for $C$ part and for $L+R$ part: $$ \frac{I_C}{i\omega C} = (I - I_C) (i\omega L + R) $$
2. $U_{in}$ is sum of voltages across the LC-circuit, $C_{in}$ capacitor and $C_{gr}$ capacitor: $$ U_{in} = \frac{I}{i\omega C_{in}} + \frac{I_C}{i\omega C} + \frac{I}{i\omega C_{gr}} $$
3. $U_{out}$ is smaller then $U_{in}$ be voltage drop on the $C_{in}$ capacitor: $$ U_{out} = U_{in} - \frac{I}{i\omega C_{in}} $$
After solving these equations we have: $$ U_{out} = U_{in}\left\{ 1 - \left[ 1 + \frac{C_{in}}{C} \frac{i\omega L + R}{ i\omega L + R + 1/(i\omega C)} + \frac{C_{in}}{C_{gr}} \right]^{-1} \right\} $$
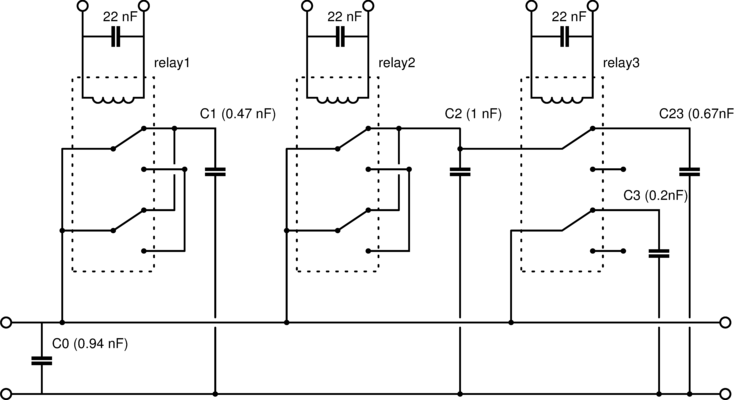
Python program for calculating resonances: rota_nmr/plot_nmr. Curves 0..8 correspond to all combinations of relays 1,2,3 (see below).
Many parameters in $^3$He-B have well-known dependence on magnetic field, it's good to do experiments as a function of it. We did a board with three latching relays to have 8 different frequencies (553, 588, 623, 674, 710, 742, 789, 833 kHz).
Later (in 2016) I did similar relay box for DryDemag cryostat.
